Answer:
![[\psi]= [Length^(-3/2)]](https://img.qammunity.org/2020/formulas/physics/college/19stw58bjxf2oqrjhsusn0d79kal39xlpx.png)
- This means that the integral of the square modulus over the space is dimensionless.
Step-by-step explanation:
We know that the square modulus of the wavefunction integrated over a volume gives us the probability of finding the particle in that volume. So the result of the integral
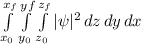
must be dimensionless, as represents a probability.
As the differentials has units of length
![[dx]=[dy]=[dz]=[Length]](https://img.qammunity.org/2020/formulas/physics/college/6xapp01qa5f45qcb8sm5ga1z89o3ujmv79.png)
for the integral to be dimensionless, the units of the square modulus of the wavefunction has to be:
![[\psi]^2 = [Length^(-3)]](https://img.qammunity.org/2020/formulas/physics/college/b2p1foo9tst0vibvkpstrw1mqc9uw3j368.png)
taking the square root this gives us :
![[\psi] = [Length^(-3/2)]](https://img.qammunity.org/2020/formulas/physics/college/hlilw5vmvsvdz2caiqzx134up0aze6wwxf.png)