Question

Identify the minimum value of the function y = 2x2 + 4x
Answer

Answer 1

(-1, -2)

Explanation:

Find the x-value the minimum occurs at. Use this value to find the minimum value. (Graph to find the highest point)

Answer 2

y = - 2 is the minimum value

Explanation:

The minimum value is the y- coordinate of the vertex.

The vertex lies on the axis of symmetry which is positioned at the midpoint of the zeros.

To find the zeros let y = 0, that is

2x² + 4x = 0 ← factor out 2x on the left side

2x(x + 2) = 0

Equate each factor to zero and solve for x

2x = 0 ⇒ x = 0

x + 2 = 0 ⇒ x = - 2

midpoint =
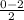`(0-2)/(2)` = - 1 ← x- coordinate of vertex

Substitute x = - 1 into the equation for corresponding y- coordinate

y = 2(- 1)² + 4(- 1) = 2 - 4 = -2

vertex = (- 1, - 2)

Hence minimum value = - 2