Question

Need help for solving for a radical function

Answer 1

Graph the following points: (-4, 0), (-3, 2), (0, 4)

Domain:
`x\geq -4`

Range:
`y\geq 0`

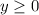
Explanation:

The parent function of
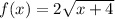`f(x)=2√(x+4)` is
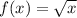`f(x)=√(x)`. The 2 on the outside of the square root tells us that the parent graph will undergo a vertical stretch of 2. The +4 is really -(-4) so it is a negative four, therefore the parent function will horizontally shift to the left by 4 units.

Start by creating a t-chart with a few points from the parent function,
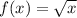`f(x)=√(x)`, on the left side then on the right side you'll transform the points from the parent function.

The left side of the t-chart should have the following points:

• (0, 0)
• (1, 1)
• (4, 2)

Notice how there are no negative x-values because this is a square root function, and you cannot take the root of a negative number (it would be imaginary and not graphable in this kind of graph).

The right side of the t-chart should have the following points:

• (-4, 0)
• (-3, 2)
• (0, 4)

I got these points by multiplying the y-values by the vertical stretch, 2, and subtracting 4 from the x-values to accomplish the horizontal stretch.

Note that everything outside of the "parentheses" (square root incl.) would be a vertical stretch/compression/shift, and everything inside the "parentheses" would be a horizontal stretch/compression/shift.

To solve your problem you would graph the right side of the t-chart because that is the transformed parent function.

Now for the domain and range:

The domain of the parent square root function is always going to be
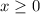`x\geq 0`. If you think about it, it makes sense since you cannot use any x-values less than 0 otherwise you'd come up with an imaginary number.

However, since this square root function is horizontally shifted 4 units to the left, the domain would start at -4. So the domain for this graph is:
`x\geq -4`.

The range is the same; when you take the square root of a positive number you will not get a negative number. Therefore the range is also
`y\geq 0`.

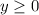I've attached a picture of what the graph should look like.