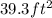Question

To the nearest tenth, what is the area of the shaded segment when BN = 8 ft?

A)22.6 ft2

B)53.2 ft2

C)39.3 ft2

D)72.8 ft2

Answer 1

The area of the shaded segment is approximately
`39.3 ft^(2)`

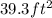
Solution:

Note: Refer the image attached below.

As given, BN = 8 ft

So radius r = 8

The angle c =
`120^(\circ)`

We know that the area of the shaded part is
`=\left((r^(2))/(2)\right) *\left(\left((\pi)/(180)\right) * c-\sin (c)\right)`

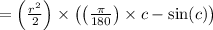
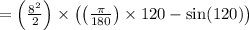`=\left((8^(2))/(2)\right) *\left(\left((\pi)/(180)\right) * 120-\sin (120)\right)` (// putting the value of r and c

)

`=\left((64)/(2)\right) *\left(\left((\pi)/(180) * 120\right)-\left((√(3))/(2)\right)\right)` (// putting value of sin⁡(120))

`=32 *\left((2 \pi)/(3)-\left((√(3))/(2)\right)\right)`

`=32 *\left((4 \pi-3 √(3))/(6)\right)`

`=\left((16)/(3)\right) *(4 \pi-3 √(3))`

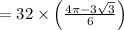
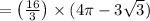
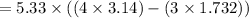`=5.33 *((4 * 3.14)-(3 * 1.732))` (//putting value of π and √3 )

`=5.33 *(12.56-5.196)`

`=5.33 * 7.36`

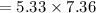
= 39.2288 which is approximately, 39.3

So, the area of the shaded part is
`39.3 ft^(2)`