Question

5. The width of a row of identical townhouses,

y, and the number of townhouses, x, have
a proportional relationship. The width of
5 townhouses is 105 ft.
a. What is the constant of proportionality?
b. Write an equation that relates the width
of a row of townhouses and the number
of townhouses.​

Answer 1

a. The value of the constant k is 21

b. The equation is y = k * x, where k is the proportionality constant, "x" is the number of terraced houses and "y" is the width of a row of identical houses.

Explanation:

a.

A proportional relationship satisfies the equation y = k * x, where k is a positive constant and is called a proportionality constant. In this case "x" is the number of terraced houses and "y" is the width of a row of identical houses.

The data you have is that the width of 5 townhouses are 105 feet. This means that the value of "x" is 5 houses and the value of "y" is 105 feet. By replacing in the equation y = k * x and isolating the constant k, you get:

105=k*5

`k=(105)/(5)`

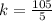
k=21

So the value of the constant k is 21.

b.

As mentioned, the equation is y = k * x, where k is the proportionality constant, "x" is the number of terraced houses and "y" is the width of a row of identical houses.

This means that just as "x" increases, "y" increases. And that if "x" decreases, "y" will decrease. And this relationship between "x" e "and" will always be the same, determined by the value of the constant "k".