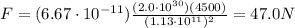Question

What is the force of gravity (in Newtons) acting between the Sun and a 4,500-kg rocket that is 0.75 AU from the Sun?

Answer 1

47.0 N

Step-by-step explanation:

First of all, let's convert the distance of the rocket from the Sun from AU to metres:

`r = 0.75 AU \cdot 1.5 \cdot 10^(11) =1.13\cdot 10^(11) m`

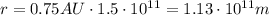
The force of gravity acting between the Sun and the rocket is:

`F=G(Mm)/(r^2)`

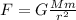
where

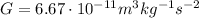`G=6.67\cdot 10^(-11) m^3 kg^(-1) s^(-2)` is the gravitational constant

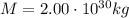`M=2.00\cdot 10^(30) kg` is the mass of the Sun

m = 4500 kg is the mass of the rocket

r is the distance between the Sun and the rocket

Substituting into the equation,

`F=(6.67\cdot 10^(-11)) ((2.0\cdot 10^(30))(4500))/((1.13\cdot 10^(11))^2)=47.0 N`