Answer:
The answers are A , C , D
Explanation:
Lets revise the rule of exponent
*
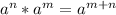
*
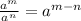
*
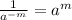
*
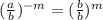
Now lets solve the problem
We need all the expressions equivalent to
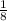
A.
∵
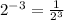
∵ 2³ = 8
∴
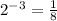
Answer A is equivalent to
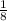
B.
∵ 2³ = 8
Answer B is not equivalent to
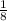
C.
∵ 2³ = 8
∴

Answer C is equivalent to
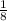
D.
∵
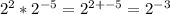
∵
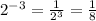
Answer D is equivalent to
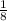
E.
∵
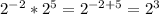
∵ 2³ = 8
Answer E is not equivalent to
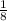
The answers are A , C , D