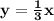Answer:
Equation of the line passing through points (6, 2) , (0, 0) is
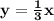
Solution:
Equation of line passing through two points
 is given as,
is given as,
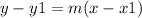 --- eqn 1
--- eqn 1
Where m is slope of line AB and value of m is given as
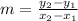
By substituting the value of “m” in eqn 1, we get
 ----- eqn 2
----- eqn 2
From question, given that two points are (6, 2), (0, 0).
Hence we get

By substituting the values in eqn 2,
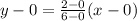
On simplifying above equation,
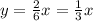
Hence equation of the line having points (6, 2) and (0, 0) is