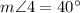Question

The mAngle6 = (11x + 8)° and mAngle7 = (12x – 4)° Parallel lines x and y are cut by transversal w. On line x where it intersects with line w, 4 angles are created. Labeled clockwise, from uppercase left, the angles are: 2, 4, 3, 1. On line y where it intersects with line w, 4 angles are created. Labeled clockwise, from uppercase left, the angles are: 6, 8, 7, 5. What is the measure of Angle4? mAngle4 = 40° mAngle4 = 48° mAngle4 = 132° mAngle4 = 140°

Answer 1

angle 4.40

Explanation:

Answer 2

`m\angle 4=40^(\circ)`

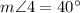
Explanation:

Angles 6 and 7 are vertical angles (opposit to each other). Vertical angles are congruent, so

`11x+8=12x-4\\ \\11x-12x=-4-8\\ \\-x=-12\\ \\x=12`

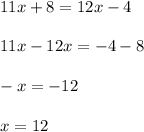
Now,

`m\angle 6=(11\cdot 12+8)^(\circ)=140^(\circ)\\ \\m\angle 7=(12\cdot 12-4)^(\circ)=140^(\circ)`

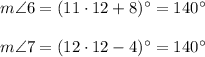
Angles 6 and 8 are supplementary angles (add up to 180°), so

`m\angle 8=180^(\circ)-140^(\circ)=40^(\circ)`

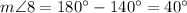
Angles 8 and 4 are corresponding angles. Corresponding angles are congruent, so

`m\angle 4=40^(\circ)`