Answer: 0.522 m
Step-by-step explanation:
This situation is related to projectile motion, where the initial velocity of the car
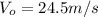 has only the horizontal component. This means the angle is equal to zero (
has only the horizontal component. This means the angle is equal to zero (
 ). And the equations we will use to find the height
). And the equations we will use to find the height
 of the cliff are:
of the cliff are:
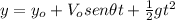 (1)
(1)
Where:
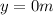 is the final height of the car
is the final height of the car
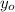 is the initial height
is the initial height
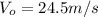 is the initial velocity of the car
is the initial velocity of the car
 is the time
is the time
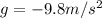 is the acceleration due to gravity
is the acceleration due to gravity
 is the angle
is the angle
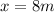 is the horizontal distance traveled by the car after passing the cliff
is the horizontal distance traveled by the car after passing the cliff
Well, firstly we have to find
 from (1):
from (1):
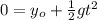 (3)
(3)
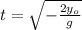 (4)
(4)
Substituting (4) in (2):
 (5)
(5)
Isolating
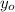 :
:
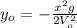 (6)
(6)
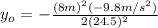 (7)
(7)
Finally:
