Question

Write an absolute value inequality that represents the situation. Then solve the inequality. The difference between the perimeters of the figures is less than or equal to 3.

Answer 1

All real numbers greater than or equal to 2.5 and less than or equal to 5.5

`2.5 \leq x \leq 5.5`

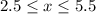
Explanation:

see the attached figure to better understand the problem

step 1

Find the perimeter of the square

The perimeter of the square is

`P=4(b)`

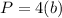
where

b is the length side of the square

substitute the given value

`P=4(x)=4x\ units`

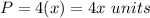
step 2

Find the perimeter of rectangle

The perimeter of rectangle is

`P=2(L+W)`

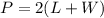
where

L is the length of rectangle

W is the width of rectangle

substitute the given values

`P=2[(x+1)+3]`

`P=2[x+4]`

`P=(2x+8)\ units`

step 3

we know that

The difference between the perimeters of the figures is less than or equal to 3

Write an absolute value inequality that represents the situation

`\left|4x-\left(2x+8\right)\right|\le 3`

`\left|\left(2x-8\right)\right|\le3`

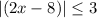
Solve the absolute value

First case (positive value)

`+(2x-8)\le 3`

`2x\le 3+8`

`2x\le 11`

`x\le 5.5`

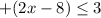
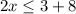
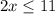
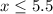
The solution is the interval -----> (-∞,5.5]

Second case (negative value)

`-(2x-8)\le 3`

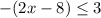
Multiply by -1 both sides

`(2x-8)\ge -3`

`2x\ge -3+8`

`2x\ge 5`

`x\ge 2.5`

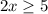
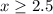
The solution is the interval -----> [2.5,∞)

The solution of the absolute value for x is

[2.5,∞) ∩ (-∞,5.5] =[2.5,5.5]

`2.5 \leq x \leq 5.5`

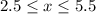
All real numbers greater than or equal to 2.5 and less than or equal to 5.5