Answer:
The simplest form is
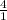 or 4
or 4
Solution:
Given,
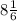 divided by
divided by
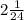
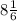
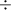
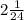
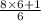
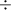
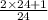
we get,
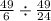
When two terms are in division, we have to reciprocate the second term,
The reciprocal of
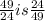
Substituting the reciprocal form of
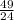 in the equation we get,
in the equation we get,

On dividing the possible terms we get,
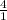
The simplest form of the given value is
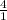 or 4
or 4