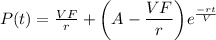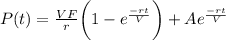Answer:
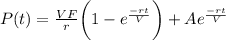
Explanation:
We are given that pollution in a lake is given by the differential equation:
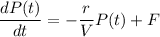
where, P(t) is the pollution at time t, r is the flow rate, V is the volume of lake and F is the mass of pollution dumped.
The given differential equation can be written as:
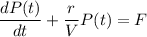
Comparing to linear differential equation:
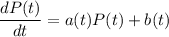 ,
,
we get,
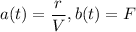
Integrating factor:
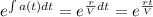
Solution:
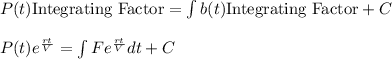
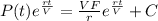 ,
,
where C is the constant of integration.
Now, we are given that P(0) = A
putting these value in the above equation, we get,
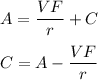
Putting this value of C in equation, we get:
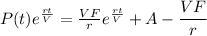
Dividing the equation by
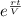 , we get:
, we get: