Answer with Step-by-step explanation:
We know that the components of velocity are obtained from position as
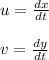
Using the given values we obtain
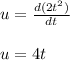
Similarly
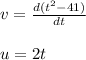
The the velocity function can be written as
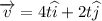
The components of acceleration are obatined from the components of velocity as
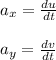
Using the given values we obtain
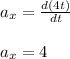
Similarly
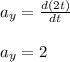
The the acceleration function can be written as

Thus at time 't=1' the velocity function becomes
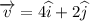
Thus the component of acceleration in the direction of the given vector
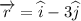 can be found by taking the dot product of the 2 vectors
can be found by taking the dot product of the 2 vectors
Thus we get
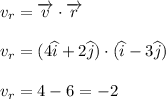
Similarly the dot product is obtained for acceleration as
