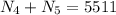Question

4 people are to be chosen from 10 men and 12 women to form a committee which contains at leat two women. How many different ways can the committee be formed? If, among the 10 men and 12 women, Mr. and Mrs. Smith can not both be selected, then how many different ways can the committee be formed?

Answer 1

the cases are N_4+N_5=5511

Explanation:

Answer 2

Answer with Step-by-step explanation:

The condition that at least 2 women are included is satisfied in the below cases:

Case 1) Exactly 2 women included

Thus the total number of ways to select the committee is

`N_1=\binom{12}{2}* \binom{10}{2}=2970`

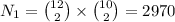
Case 2) Exactly 3 women included

Thus the total number of ways to select the committee is

`N_2=\binom{12}{3}* \binom{10}{1}=2200`

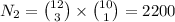
Case 3) Exactly 4 women are included

Thus the total number of ways to select the committee is

`N_3=\binom{12}{4}* \binom{10}{0}=495`

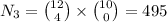
Thus the total number of commitees possible are

`N_1+N_2+N_3=2970+2200+495=5665`

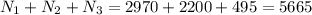
Part 2)

If Mr and Mrs Simith are not to be both included then in that case the number of ways are the sum of

1) All cases of Mr Smith included and Mrs smith excluded

`N_4=\binom{11}{2}\binom{10}{2}+\binom{11}{3}\binom{10}{1}+\binom{11}{4}\binom{10}{0}\\\\N_4=4455`

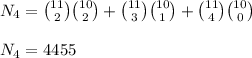
2) Mrs smith included and Mr Smith Included

`N_5=\binom{11}{1}\binom{9}{2}+\binom{11}{2}\binom{9}{1}+\binom{11}{3}\binom{9}{0}\\\\N_5=1056`

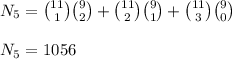
Thus the cases are
`N_4+N_5=5511`