Let
 be the line given by the vector equation
be the line given by the vector equation
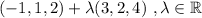 .
.
First, we use the director vectors of the lines L1 and L2 to get the
vector equation of the plane containing them, which we denote by
 . This is,
. This is,
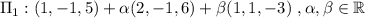
We observe that
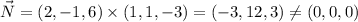 . Therefore, the vector equation of
. Therefore, the vector equation of
 defines a plane and
defines a plane and
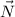 is a normal vector to
is a normal vector to

Finally, the vector equation for the wanted plane, which we denote by
 , is
, is
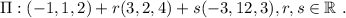
Thus, if
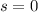 , then
, then
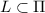 and since
and since
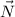 is parallel to
is parallel to
 , then it is perpendicular to
, then it is perpendicular to
 .
.