Answer:
inf(A) does not exist.
Explanation:
As per the question:
We need to prove that A is closed under multiplication,
If for every
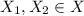
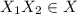
Proof:
Suppose, x, y
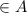
Since, both x and y are real numbers thus xy is also a real number.
Now, consider another set B such that:
B = {xy} has only a single element 'xy' and thus [B] is bounded.
Since, [A] represents the union of all the bounded sets, therefore,

⇒ xy
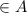
Therefore, from x, y
![\]in A](https://img.qammunity.org/2020/formulas/mathematics/college/aiczw2zajmacb49v9uez7ny8xgy9d0mzmb.png) , we have xy
, we have xy
![\]in A](https://img.qammunity.org/2020/formulas/mathematics/college/aiczw2zajmacb49v9uez7ny8xgy9d0mzmb.png) .
.
Hence, set a is closed under multiplication.
Now, to prove whether inf(A) exist or not
Proof:
Let us assume that inf(A) exist and inf(A) =
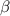
Thus
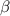 is also a real number.
is also a real number.
Let C be another set such that
C = {
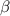 - 1}
- 1}
Now, we know that C is a bounded set thus {
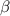 - 1} is also an element of A
- 1} is also an element of A
Also, we know:
inf(A) =
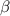
Therefore,
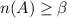
But
 is an element of A and
is an element of A and
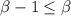
This is contradictory, thus inf(A) does not exist.
Hence, proved.