Question

A 4-ft tall, 8-in wide concrete (150lb/ft3)

retainingwall is built. During a heavy rain, water fills the

spacebetween the wall and the earth behind it to a depth, h.

Determine the maximum depth of water possible without the

walltipping over. The wall simply rests on the ground withoutbeing

anchored to it.

Answer 1

maximum possible height of water is 2.34 ft without wall tipping

Step-by-step explanation:

given data

wall height = 4 ft

wall width = 8 in = 0.667 ft

weight density = 150 lb/ft³

to find out

the maximum depth of water possible without the wall tipping

solution

we find here first weight of concrete wall that is

weight = volume × weight density

weight = length × width × height × weight density

weight = 150 × 4 × 0.667 × L

weight = 400 L lb

here L is length

now find the resulting force acting due to hydrostatic force per unit length

Fr = density of water × hc × ( h×L)

heer hc is distance between fluid surface and centroid area =
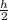`(h)/(2)` and L is length and h is height

and density of water is 62.4 lb/ft³

so Fr = 62.4 ×
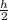`(h)/(2)` × ( h×L)

Fr = 31.2 h²L

now

point of position of apply resultant force that is Yr

Yr =
`(moment interia)/(hc* area) + hc`

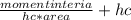
Yr =
`(L*(h^3)/(12))/((h)/(2) * h*L) + (h)/(2)`

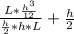
Yr =
`(2h)/(3)`

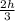
so

moment about about point A will be zero to avoid tapping

so

∑Ma = 0

`W*(0.667)/(2) - Fr*( h -Yr ) = 0`

`400*(0.667)/(2) - 31.2 h^2 * ( h -(2h)/(2)) = 0`

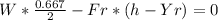
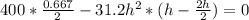
h = 2.34

so maximum possible height of water is 2.34 ft without wall tipping