Answer and Solution:
As per the question:
Given:
If
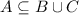

To prove:
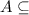
Proof:
Suppose

As we know that:
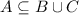
Therefore,
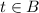 or
or
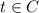
Now, if we assume that
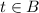
Then
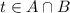
Since,
 and
and
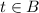
But
A and B are disjoint set and

Therefore, this is contradictory.
Thus
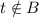
So,
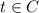
Every element in the set A is also present in the set C
Therefore,
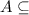
Hence, proved.