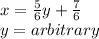Question

Use the Gauss-Jordan method to solve the following system of equations. 6х - 5у%3D7 12x 10y 14 - Select the correct choice below and, if necessary, fill in the answer box to complete your choice. OA. The solution is (Type an ordered pair. Simplify your answer) O B. There are infinitely many solutions. The solution is (Simplify your answer. Use integers or fractions for any numbers in the expression.) y.where y is any real number O C. There is no h solution

Answer 1

The system
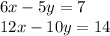`6x-5y=7\\12x-10y=14` has infinitely many solutions
`x=(5)/(6)y +(7)/(6)\\y=arbitrary`

Explanation:

We have the following system of equations:

`6x-5y=7\\12x-10y=14`

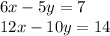
The augmented matrix of the system is:

`\left[\begin{array}c6&-5&7\\12&-10&14\end{array}\right]`

Transform the augmented matrix to the reduced row echelon form

• Row Operation 1: multiply the 1st row by 1/6

`\left[\begin{array}c1&-5/6&7/6\\12&-10&14\end{array}\right]`

• Row Operation 2: add -12 times the 1st row to the 2nd row

`\left[\begin{array}cc1&-5/6&7/6\\0&0&0\end{array}\right]`

From the reduced row echelon form of the augmented matrix we have the corresponding system of linear equations:

`x-(5)/(6)y=(7)/(6)\\0=0`

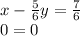
The last row of the system (0 = 0) means that the system has infinitely many solutions.

`x=(5)/(6)y +(7)/(6)\\y=arbitrary`