Question

The following exercise uses Heron's formula. Find the area of a garden that is a triangle with sides 6 feet, 7 feet, and feet. (Round your answer to one decimal place)

Answer 1

20.3 square feet.

Explanation:

We have been given the sides of a garden. We are asked to find the area of garden using Heron's formula.

The area of a triangle with sides a, b and c would be:

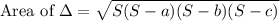`\text{Area of }\Delta=√(S(S-a)(S-b)(S-c))`, where S is the semi-perimeter of triangle.

Let us find semi-perimeter as:

`S=(6+7+8)/(2)=(21)/(2)=10.5`

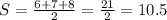
Substitute given side lengths:

`\text{Area of garden}=√(10.5(10.5-6)(10.5-7)(10.5-8))`

`\text{Area of garden}=√(10.5(4.5)(3.5)(2.5))`

`\text{Area of garden}=√(413.4375)`

`\text{Area of garden}=20.333162`

`\text{Area of garden}\approx 20.3`

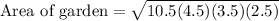
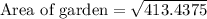
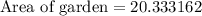
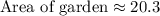
Therefore, the area of the garden would be 20.3 square feet.