Question

* 4. Prove the following: If (G, *, e) is a finite group with even order, then there exists g Fe in G such that g*g=e.

Answer 1

As (G, *, e) is a group with 2n elements, we have 2n-1 elements different from e. Let us assume that there aren't elements of (G, *, e) such that g*g=e. Now, take pairs of elements of (G, *, e) as
`(g,g^(-1))`, i.e., let us associate each element (different from e) with its multiplicative inverse. Let us remark that we are making no distinction between
`(g,g^(-1))` and
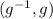`(g^(-1),g)`, because they essentially the same pair.

Now, how many different pairs can we form with 2n-1 elements? Only n-1, which give us 2n-2 elements. Then, there is a ‘‘missing’’ element of that list. That element must fulfill that g*g=e, because it cannot be paired with any other element.