Answer:
Here I will assume that
 is the vector space of functions
is the vector space of functions
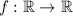 . If
. If
 is the space of continuous functions, there will be no changes in the proof, because polynomial functions are also continuous.
is the space of continuous functions, there will be no changes in the proof, because polynomial functions are also continuous.
Let us write
 for the set of polynomials with real coefficients. As we want to prove that
for the set of polynomials with real coefficients. As we want to prove that
 is a subspace of
is a subspace of
 we need to check three conditions:
we need to check three conditions:
First:
 is a non empty set, in particular
is a non empty set, in particular
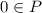 . This is not difficult, because the function identically 0 is a polynomial. Then,
. This is not difficult, because the function identically 0 is a polynomial. Then,
 is not empty and contains the 0 vector of
is not empty and contains the 0 vector of
 .
.
Second: The addition of two elements of
 stays in
stays in
 . Consider two arbitrary polynomials
. Consider two arbitrary polynomials
 and
and
 . Then,
. Then,
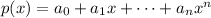
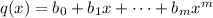 .
.
This means that
 is a polynomial of degree
is a polynomial of degree
 with coefficients
with coefficients
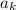 , and
, and
 is a polynomial of degree
is a polynomial of degree
 with coefficients
with coefficients
 . With out lose of generality assume that
. With out lose of generality assume that
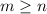 .
.
Now, notice that

which is a polynomial too.
Hence,
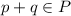 .
.
Third: The multiplication by a scalar stays in
 .
.
Consider an arbitrary polynomial
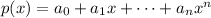
and a real number
 .
.
Then,
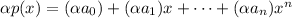
which is a polynomial.
Hence,
 .
.
Therefore,
 is a subspace of the vector space
is a subspace of the vector space
 .
.