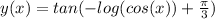Question

Use separation of variables to solve dy dx − tan x = y2 tan x with y(0) = √3. Find the value of c in radians, not degrees

Answer 1

`y(x)=tan(-log(cos(x))+(\pi )/(3) )`

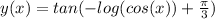
Explanation:

Rewrite the equation as:

`(dy(x))/(dx)-tan(x)=y(x)^(2) *tan(x)`

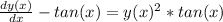
Isolating
`(dy)/(dx)`

`(dy)/(dx) =tan(x)+tan(x)*y^(2)`

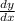
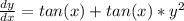
Factor:

`(dy)/(dx) =tan(x)*(1+y^(2) )`

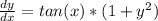
Dividing both sides by
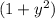`(1+y^(2) )` and multiplying them by
`dx`

`(dy)/(1+y^(2) ) =tan(x)dx`

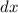
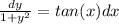
Integrate both sides:

`\int\ (dy)/(1+y^(2) ) = \int\ tan(x)  dx`

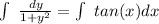
Evaluate the integrals:

`arctan(y)=-log(cos(x))+C_1`

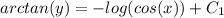
Solving for y:

`y(x)=tan(-log(cos(x))+C_1)`

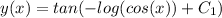
Evaluating the initial condition:

`y(0)=√(3) =tan(-log(cos(0))+C_1)=tan(-log(1)+C_1)=tan(0+C_1)`

`√(3) =tan(C_1)\\arctan(√(3) )=C_1\\60=C_1`

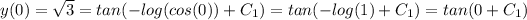
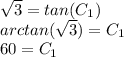
Converting 60 degrees to radians:

`60degrees*(\pi )/(180degrees) =(\pi )/(3)`

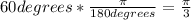
Replacing
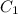`C_1` in the diferential equation solution:

`y(x)=tan(-log(cos(x))+(\pi )/(3) )`