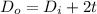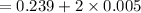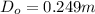Question

A cylindrical tank must be designed to contain 5 kg of compressed nitrogen at a pressure of 200 atm (gage) and 20°C. The design constraints are that the length must be twice the diameter and the wall thickness must be 0.5 cm. What are the external dimensions?

Answer 1

`D_o = 0.249 m`

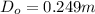
Step-by-step explanation:

Given data:

Mass of cylinder is 5 kg

Pressure = 200 atm

Temperature = 20 degree celcius = 293 K

wall thickness = 0.5 cm = 0.005 m

we know that Gas constant for nitrogen is calculated as

`\frac{\bar{R}}{M}`

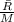
`R = (8314)/(28.01) = 296.82 J/kg.K</p><p>FROM IDEAL GAS EQUATION</p><p>PV =mRT</p><p>[tex]V = (mRT)/(P)`

`= \FRAC{5* 296.82* 293}{200* 101325}`

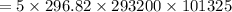
V = 0.021457 m^3

internal diameter by using volume formula

`V =(\pi)/(4) D_i^2 L`

`0.021457 = (\pi)/(4) D_i^2 (2D_i)`

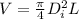
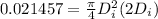
solving for
`D_i`

`D_i = 0.239 m`

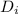
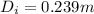
calculate the outer diameter

`D_o = D_i + 2t`

`= 0.239  + 2* 0.005`

`D_o = 0.249 m`