Answer:
19 minutes
Explanation:
Let x be the number of minutes the call lasts.
The first three minutes of a call cost $2.00.
Then
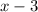 minutes left.
minutes left.
Each additional minute or portion of a minute of that call costs $0.50, so
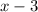 minutes cost
minutes cost
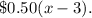
The total cost is
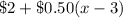
The price of the call is $10.00, so the maximum number of minutes one can call long distance for $10.00 can be calculated from the inequality
![2+0.50(x-3)\le 10\\ \\20+5(x-3)\le 100\ [\text{Multiplied by 10}]\\ \\20+5x-15\le 100\\ \\5x+5\le 100\\ \\5x\le 100-5\\ \\5x\le 95\\ \\x\le 19](https://img.qammunity.org/2020/formulas/mathematics/high-school/2g0awn2n1w50xov3t4p6sugqvw7wpl6anq.png)
When x=19, the cost of the call is $10.00. When x<19, then the price of the call is less than $10.00.