Answer:
The interpolating polynomial is
 .
.
Explanation:
We want to find a quadratic polynomial
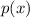 such that
such that
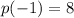 ,
,
 and
and
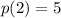 . In order to do this let us write
. In order to do this let us write
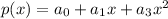 .
.
Now, evaluating the polynomial in the points -1, 1 and 2 we get
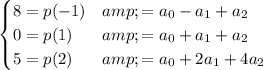
This relations give us a linear system of equations:
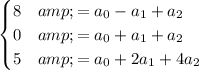
where the
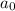 ,
,
 and
and
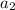 are the unknowns.
are the unknowns.
The augmented matrix of the system is

In this matrix it is easy to eliminate the 1's of the first column and get
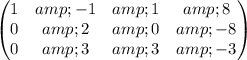
From this matrix we can find the values of each unknown. Notice that the second row gives us
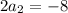 that yields
that yields
 .
.
Then, the third row means
 that gives
that gives
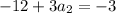 . So,
. So,
 .
.
Finally, the first row is
 and substituting is
and substituting is
 that yields
that yields
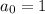 .
.
Therefore, the interpolating polynomial is
 .
.