Answer with Step-by-step explanation:
Let us assume the 2 consecutive natural numbers are 'n' and 'n+1'
Thus the product of the 2 numbers is given by
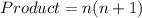
We know that the sum of 'n' consecutive natural numbers starting from 1 is
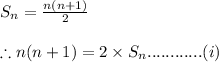
Thus from equation 'i' we can write
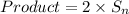
As we know that any number multiplied by 2 is even thus we conclude that the product of 2 consecutive numbers is even.