Question

(1) Find the torsion of the helix a(t) = (cos(t), sin(t), t)

Answer 1

The torsion of the helix is
`\tau=(1)/(2)`.

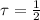Explanation:

To complete this exercise we need to recall the formula for the torsion of a curve. Given a parametrization
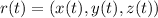`r(t) = (x(t), y(t), z(t))` the torsion of the curve is given by

`\tau = ((r'* r'')\cdot r''')/(\|r'* r''\|^2)`.

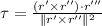So, the first step is to find the derivatives of the vector function
`r`.

Thus,

`r(t)=(\cos t,\sin t, t)`,

`r'(t) = (-\sin t, \cos t, 1)`,

`r''(t) = (-\cos t, -\sin t, 0)`,

`r'''(t)=(\sin t, -\cos t,0)`.

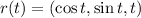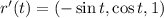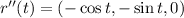Now, we must calculate the cross product of the vector functions
`r'` and
`r''`.

`r'(t)* r''(t)=\begin{vmatrix}i& j & k\\ -\sin t & \cos t & 1\\ -\cos t & -\sin t & 0\end{vmatrix} = i\begin{vmatrix} \cos t & 1\\ -\sin t & 0\end{vmatrix} -j\begin{vmatrix} -\sin t & 1\\ -\cos t & 0\end{vmatrix}+k\begin{vmatrix} -\sin t & \sin t\\ -\cos t & -\sin t\end{vmatrix}`

`r'(t)* r''(t) = i\sin t -j\cos t +k(\sin^2t+\cos^2t) = i\sin t -j\cos t +k`.

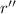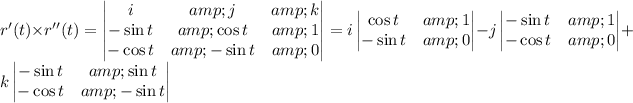
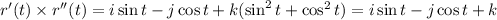Now we calculate
`\|r'* r''\|^2`:

`\|r'* r''\|^2 = \sin^2t+\cos^2t+1=2`

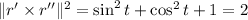
Recall that the norm of a vector in the space
`\mathbb{R}^3` is

`\|(x,y,z)\|^2 = x^2+y^2+z^2`.

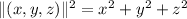At this point we have

`\tau = (1)/(2)\left((i\sin t -j\cos t +k)\cdot (i\sin t -j\cos t+0k)\right) = (1)/(2)\left(\sin^2t+\cos^2t\right) =(1)/(2)`.