Answer: Hello there!
A model to see the growth of a certain population is the exponential model.
If the initial population is P, then the model can be written as
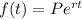
Where t is the time, and r is growth rate.
and f(0) = P
Then we want to know the time needed for the initial population to be doubled, this is f(x) = 2P, where x is the time that we want to find.
then
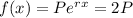
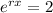
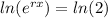
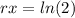
then x= ln(2)/r