Answer:
a) V(2) = 0 The particle is at rest
b) The maximum displacement is 1m
Explanation:
Let's first find velocity and displacement from the given acceleration:
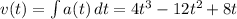
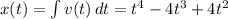
Now we need the instant t1 where x(t1) = 0 and then we evaluate v(t1) to find its velcity and verify if it is 0:
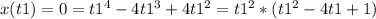 Solving for t, we get:
Solving for t, we get:
t1 = 0 and t1 = 2s Now we evaluate v(2):
v(2) = 0m/s It is at rest when it returns to x=0m
Now, for maximum displacement, we need the instant when v(tm) = 0
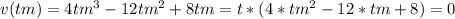 Solving for tm:
Solving for tm:
tm=0; tm = 1 and tm = 2
Since x(0) and x(2) are both 0, we calculate x(1) to find the maximum displacement:
x(1) = 1m