Answer:2584.52 mm
Step-by-step explanation:
Given
Velocity is given=436-15t
V is in mm/s
and we know
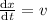
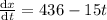
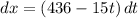
Integrating both sides we get
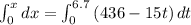

x=2584.52 mm
Here distance is equal to displacement because from graph area under the v -t graph gives displacement when we consider sign and distance if we take absolute values