Answer:
The displacement from t = 0 to t = 10 s, is -880 m
Distance is 912 m
Step-by-step explanation:
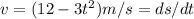 . . . . . . . . . . A
. . . . . . . . . . A
integrate above equation we get

from information given in the question we have
t = 1 s, s = -10 m
so distance s will be
-10 = 12 - 1 + C,
C = -21
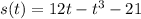
we know that acceleration is given as
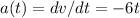
[FROM EQUATION A]
Acceleration at t = 4 s, a(4) = -24 m/s^2
for the displacement from t = 0 to t = 10 s,
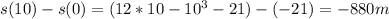
the distance the particle travels during this time period:
let v = 0,
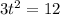
t = 2 s
Distance
![= [s(2) - s(0)] + [s(2) - s(10)] = [1* 2 - 2^3] + [(12* 2 - 2^3) - (12* 10 - 10^3)] = 912 m](https://img.qammunity.org/2020/formulas/engineering/college/gbdm9aht0btrh0n2i2e1zq1rhfkca8jjn6.png)