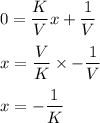Question

studying enzyme kinetics encounter formulas of the form f(x) = (K/V)x+1/V, where and are constants. Use this infombon to answer parts and (b). (a) If f(x) = 0.9x + 10, find K and V so that f(x) may be written in the form f(x) = (K/V)x+ 1/V. (b) Find the x-intercept and y-intercept of the line y - (K/V)x+1/V (in terms of K and V). (a) K= (Simplify your answer. Type an integer or a fraction.)

Answer 1

a) K = 0.09, V = 0.1

b)

`y-intercept= \displaystyle(1)/(V)`

`x-intercept= -\displaystyle(1)/(K)`

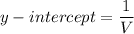
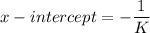
Explanation:

We are given that:

`f(x) = \displaystyle(K)/(V)x + \displaystyle(1)/(V)`

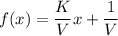
a) If we compare the above equation with the given equation:

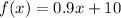`f(x) = 0.9x +10`, then, we get:

`\displaystyle(1)/(V) = 10\\\\V = \displaystyle(1)/(10) = 0.1\\\\\displaystyle(K)/(V) = 0.9\\\\K* \displaystyle(1)/(0.1) = 0.9\\\\K = 0.09`

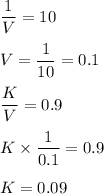
K = 0.09, V = 0.1

b)
`f(x) = \displaystyle(K)/(V)x + \displaystyle(1)/(V)`

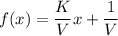
y-intercept is the value when x = 0. Putting x = 0,

`y-intercept= \displaystyle(1)/(V)`

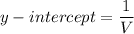
x-intercept is the value when y = 0. Putting y = 0, we get,

`0 = \displaystyle(K)/(V)x + \displaystyle(1)/(V)\\\\x = \displaystyle(V)/(K)* -\displaystyle(1)/(V)\\\\x = -\displaystyle(1)/(K)`