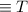Answer:
The statement
![P \leftrightarrow [(\lnot P) \rightarrow (Q \land \lnot Q)]](https://img.qammunity.org/2020/formulas/mathematics/college/8q1p10yv1sik8mtdp5zrdx2wystxxwi6dm.png) is a tautology.
is a tautology.
Explanation:
A tautology is a formula which is "always true" that is, it is true for every assignment of truth values to its simple components.
To show that this statement is a tautology we are going to use a table of logical equivalences:
![P \leftrightarrow [(\lnot P) \rightarrow (Q \land \lnot Q)] \equiv](https://img.qammunity.org/2020/formulas/mathematics/college/40vpu1pgc6gr0ehkc7q88419oxwsynl702.png)
![\equiv (P \land [(\lnot P)\rightarrow (Q \land \lnot Q)]) \lor(\lnot P \land \lnot [(\lnot P)\rightarrow (Q \land \lnot Q)])](https://img.qammunity.org/2020/formulas/mathematics/college/glqn45e6912fviw84jegvbtblw0h9jaec3.png) by the logical equivalences involving bi-conditional statements
by the logical equivalences involving bi-conditional statements
![\equiv (P \land [\lnot(\lnot P)\lor (Q \land \lnot Q)]) \lor(\lnot P \land \lnot [\lnot(\lnot P)\lor (Q \land \lnot Q)])](https://img.qammunity.org/2020/formulas/mathematics/college/cs2eozadafkx94roivg5t88ng5vz22140i.png) by the logical equivalences involving conditional statements
by the logical equivalences involving conditional statements
![\equiv (P \land [P\lor (Q \land \lnot Q)]) \lor(\lnot P \land \lnot [ P\lor (Q \land \lnot Q)])](https://img.qammunity.org/2020/formulas/mathematics/college/4fsxt9f2hp2kz08ahcqigrws9ng5ybt6kw.png) by the Double negation law
by the Double negation law
![\equiv (P \land [P\lor (Q \land \lnot Q)]) \lor(\lnot P \land \lnot P\land \lnot(Q \land \lnot Q))](https://img.qammunity.org/2020/formulas/mathematics/college/v4g40hquznwk4r95b4f7bactk5l003byok.png) by De Morgan's law
by De Morgan's law
![\equiv (P \land [P\lor F]) \lor(\lnot P \land \lnot P\land \lnot(Q \land \lnot Q))](https://img.qammunity.org/2020/formulas/mathematics/college/bvwomdytqpikt6spo4o3cphx05lv4ah9wm.png) by the Negation law
by the Negation law
![\equiv (P \land [P\lor F]) \lor(\lnot P \land \lnot P\land \lnot Q \lor \lnot(\lnot Q))](https://img.qammunity.org/2020/formulas/mathematics/college/p5q9swikn31m2x03b9mkfvbwp9857y9rjz.png) by De Morgan's law
by De Morgan's law
![\equiv (P \land [P\lor F]) \lor(\lnot P \land \lnot P\land \lnot Q \lor Q)](https://img.qammunity.org/2020/formulas/mathematics/college/qhi5bqks90icntyjrqll2dazq5agsxf5m5.png) by the Double negation law
by the Double negation law
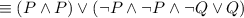 by the Identity law
by the Identity law
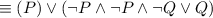 by the Idempotent law
by the Idempotent law
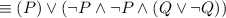 by the Commutative law
by the Commutative law
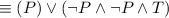 by the Negation law
by the Negation law
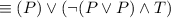 by De Morgan's law
by De Morgan's law
 by the Idempotent law
by the Idempotent law
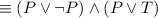 by the Distributive law
by the Distributive law
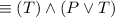 by the Negation law
by the Negation law
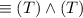 by the Domination law
by the Domination law