Question

Assume z = x + iy, then find a complex number z satisfying the given equation. d. 2z8 – 2z4 + 1 = 0

Answer 1

Answer: complex equations has n number of solutions, been n the equation degree. In this case:

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i11,25°)`

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i101,25°)`

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i191,25°)`

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i281,25°)`

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i78,75°)`

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i168,75°)`

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i258,75°)`

`Z=\frac{\sqrt[8]{2} }{\sqrt[4]{2}} e^(i348,75°)`

Explanation:

I start with a variable substitution:

`Z^(4) = X`

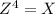
Then:

`2X^(2)-2X+1=0`

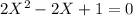
Solving the quadratic equation:

`X_(1) =(2+√(4-4*2*1) )/(2*2) \\X_(2) =(2-√(4-4*2*1) )/(2*2)`

`X=\left \{ {{0,5+0,5i} \atop {0,5-0,5i}} \right.`

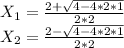
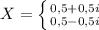
Replacing for the original variable:

`Z=\sqrt[4]{0,5+0,5i}`

or
`Z=\sqrt[4]{0,5-0,5i}`

Remembering that complex numbers can be written as:

`Z=a+ib=|Z|e^(ic)`

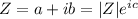
Using this:

`Z=\left \{ {{{(√(2))/(2) e^(i45°) } \atop {{(√(2))/(2) e^(i-45°) }} \right.`

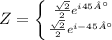
Solving for the modulus and the angle:

`Z=\left \{ {{\sqrt[4]{(√(2))/(2) e^(i45)} = \sqrt[4]{(√(2))/(2) } \sqrt[4]{e^(i45)} } \atop {\sqrt[4]{(√(2))/(2) e^(i-45)} = \sqrt[4]{(√(2))/(2) } \sqrt[4]{e^(i-45)} }} \right.`

The possible angle respond to:

`RAng_(12...n) =(Ang +360*(i-1))/(n)`

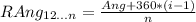
Been "RAng" the resultant angle, "Ang" the original angle, "n" the degree of the root and "i" a value between 1 and "n"

In this case n=4 with 2 different angles: Ang = 45º and Ang = 315º

Obtaining 8 different angles, therefore 8 different solutions.