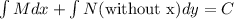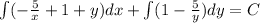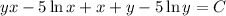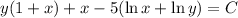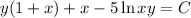Answer:
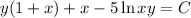
Explanation:
Consider the given differential equation is
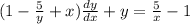
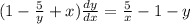
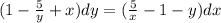
Taking all variables on right sides.
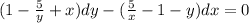
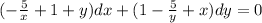
Let as assume,
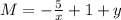 and
and
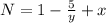
Find partial derivatives
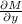 and
and

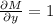 and
and
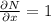
Since
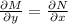 , therefore the given differential equation is exact.
, therefore the given differential equation is exact.
The solution of the exact differential equation is