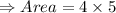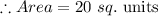Question

What is the area of a rectangle with vertices (-8, -2), (-3,-2), (-3,-6), and (-8. -6)?

square units

Answer 1

31 square units

Answer 2

The area of the rectangle is 20 sq .units.

Given:

(-8, -2), (-3,-2), (-3,-6), and (-8, -6)

Solution:

The area of the rectangle ‘A’ is given by the formula:

Area = Length × Width

Now, we have to find the sides of the rectangle.

The sides of the rectangle include s1, s2, s3, and s4.

Let’s now assume the points as:

`(x1, y1) = (-8, -2)`

`(x2, y2) = (-3,-2)`

`(x3, y3) = (-3,-6)`

`(x4, y4) = (-8, -6)`

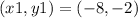
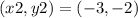
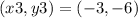
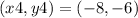
The side s1 is:

`s 1=\sqrt{(x 2-x 1)^(2)+(y 2-y 1)^(2)}`

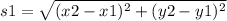
On substituting the values,

`\Rightarrow s 1=\sqrt{(-3+8)^(2)+(-2+2)^(2)}`

`\Rightarrow s 1=\sqrt{(5)^(2)+(0)^(2)}`

`\Rightarrow s 1=√(25)`

`\therefore s 1=5 \text { units }`

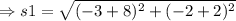
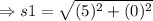
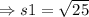
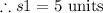
The side s2 is:

`s 2=\sqrt{(x 3-x 2)^(2)+(y 3-y 2)^(2)}`

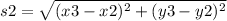
On substituting the values,

`\Rightarrow s 2=\sqrt{(-3+3)^(2)+(-6+2)^(2)}`

`\Rightarrow s 2=\sqrt{(0)^(2)+(4)^(2)}`

`\Rightarrow s 2=√(16)`

`\therefore s 2=4 \text { units }`

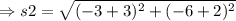
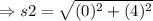
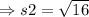
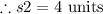
The side s3 is:

`s 3=\sqrt{(x 4-x 3)^(2)+(y 4-y 3)^(2)}`

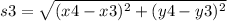
On substituting the values,

`\Rightarrow s 3=\sqrt{(-8+3)^(2)+(-6+6)^(2)}`

`\Rightarrow s 3=\sqrt{(5)^(2)+(0)^(2)}`

`\Rightarrow s 3=√(25)`

`\therefore s 3=5 \text { units }`

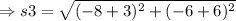
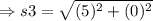
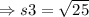
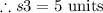
The side s4 is:

`s 4=\sqrt{(x 1-x 4)^(2)+(y 1-y 4)^(2)}`

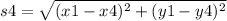
On substituting the values,

`\Rightarrow s 4=\sqrt{(-8+8)^(2)+(-2+6)^(2)}`

`\Rightarrow s 4=\sqrt{(0)^(2)+(4)^(2)}`

`\Rightarrow s 4=√(16)`

`\therefore s 4=4 \text { units }`

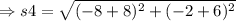
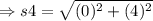
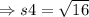
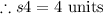
Now, the length of the given rectangle is 5 units and width of the given rectangle is 4 units.

The area of the rectangle is:

`\Rightarrow A r e a=4 * 5`

`\therefore A r e a=20 \ s q . \text { units }`