Question

Which is the irrational number?


`-(16)/(4)`,
`\sqrt[3]{64}`,
`(15)/(8)`, or
`√(26)`

Answer 1

a rational value is a value that can be expressed as a ration or fraction, so -16/4 and 15/8 are pretty much there already so we can skip those two.

now let's take a peek at the roots, ∛(64), well 4³ = 64, thus ∛(64) = ∛(4³) = 4, and we can write any integer is over 1, namely 4/1, so that's rational.

`\bf √(26)\implies √(2\cdot 13)\implies √(2)\cdot √(13)`

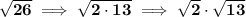
well, 2 and 13 are both prime numbers, so they can't be factored into two values that will ever give either one, so we have one irrational value, √2 times another irrational value √13 in this case, so, no way we can express those in a rational fashion.

factoid:

Ancient Greeks were aware of √2 as irrational, and kinda never liked it very much, thus they didn't deal with it much.