Question

From Euler’s relation eiθ = cosθ + isinθ,

(a) find the geometric representation of e-iθ, (b) express cosθ in terms of exponentials, (c) express isinθ in terms of exponentials.

Answer 1

(a) The graphic representation is in the attached figure.

(b)
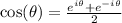`\cos(\theta) = (e^(i\theta) + e^(-i\theta))/(2)`.

(c)
`\sin(\theta) = (e^(i\theta) - e^(-i\theta))/(2i)`.

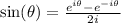Explanation:

(a) Given a complex number
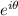`e^(i\theta)` we know, from Euler's formula that
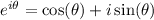`e^(i\theta) = \cos(\theta)+i\sin(\theta)`. So, it is not difficult to notice that

`|e^(i\theta)|^2 = \cos^2(\theta)+\sin^2(\theta) =1`

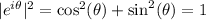
so it is on the unit circumference. Also, notice that the Cartesian representation of the complex number is
`(\cos(\theta), \sin(\theta))`.

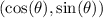Now,

`e^(-i\theta) = \cos(\theta)+i\sin(-\theta) = \cos(\theta)-i\sin(\theta)`.

Notice that
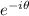`e^(-i\theta)` has the same modulus that
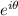`e^(i\theta)`, so it is on the unit circumference. Beside, its Cartesian representation is
`(\cos(\theta), -\sin(\theta))`.

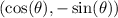So, the points
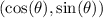`(\cos(\theta), \sin(\theta))` and
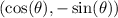`(\cos(\theta), -\sin(\theta))` are symmetric with respect to the X-axis. All this can be checked in the attached figure.

(b) Notice that

`e^(i\theta) + e^(-i\theta) = \cos(\theta)+i\sin(\theta) + \cos(\theta)-i\sin(\theta) = 2\cos(\theta)`

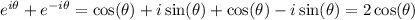
Then,

`\cos(\theta) = (e^(i\theta) + e^(-i\theta))/(2)`.

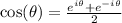(c) Notice that

`e^(i\theta) - e^(-i\theta) = \cos(\theta)+i\sin(\theta) - \cos(\theta)+i\sin(\theta) = 2i\sin(\theta)`

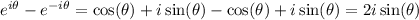
Then,

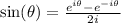`\sin(\theta) = (e^(i\theta) - e^(-i\theta))/(2i)`.