Answer:
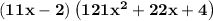
Given:

Explanation:
In this problem, we need to find the factors of the given expression.
The factors of a given number/expression are the numbers/expressions which results in given number on multiplying.
The given expression is in an algebraic expression which is:
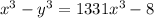
On giving the cube forms,

Now, the factored form of the above expression is:

Now,
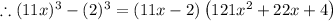
The above given is the factor for the given difference in the cube.