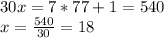Answer:
1. gcd(77,30)=1
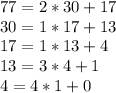
Since 1 is the last non zero remainder appearing in these equations then, 1 is the gcd of 77 and 30.
2. u=-11, v=18
Using the Euclidean Algorithm we have that
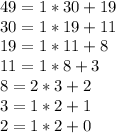
Now, we express the remainder as linear combinations of 49 and 30.
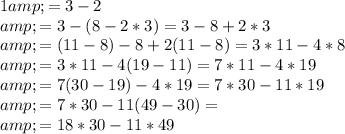
Then
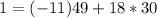
3. x=18
If
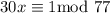 then
then
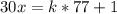 for some
for some
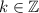 .
.
Then, if k=7,