Answer:
Let us use mathematical induction to prove the statement. So, we are going to start checking the statement for the first natural numbers.
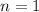 : Our set is
: Our set is
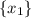 . So, obviously,
. So, obviously,
 is the maximum and minimum of our set. Then, the statement is true for
is the maximum and minimum of our set. Then, the statement is true for
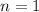 .
.
 : Our set is
: Our set is
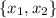 . Necessarily,
. Necessarily,
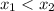 or
or
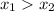 . In both cases, there is a minimum and a maximum.
. In both cases, there is a minimum and a maximum.
Once we have our statement checked for the initial cases, we state our induction hypothesis:
For every finite set A of
 elements there exists a maximum and a minimum.
elements there exists a maximum and a minimum.
Now, let us prove the that the above assertion is true for sets with
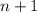 elements.
elements.
Our set is
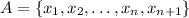 and we want to find
and we want to find
 .
.
Notice that this problem is equivalent to solve
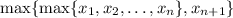 ,
,
i.e, to find the maximum among
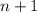 numbers, we can find first the miximum among
numbers, we can find first the miximum among
 and then compare with the other one.
and then compare with the other one.
Now, using our induction hypothesis we know that there is a maximum in the set
 , because it has
, because it has
 elements. Let us write
elements. Let us write
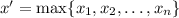 .
.
So, in order to find the maximum of A, we have to find the maximum of
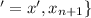 . As we have checked at the beginning, there is a maximum in
. As we have checked at the beginning, there is a maximum in
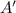 , and it is the maximum of A.
, and it is the maximum of A.
Hence, we have completed the prove for the existence of the maximum of a set with
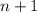 elements. The prove for the existence of the minimum is analogue, we just need to change ‘‘maximum’’ for ‘‘minimum’’.
elements. The prove for the existence of the minimum is analogue, we just need to change ‘‘maximum’’ for ‘‘minimum’’.