Question

Use the Euclidean algorithm to calculate gcd(259, 621) and gcd(108, 156).

Answer 1

The gcd(259, 621) = 1 and gcd(108, 156) = 12

Explanation:

The Euclidean algorithm solves the problem:

Given integers a, b, find d = gcd(a,b)

These are the steps of the Euclidean algorithm:

1. Let a = x, b = y.
2. Given x, y use the division algorithm to write
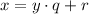   `x=y\cdot q+r` where q is quotient and r is the remainder
3. If r = 0, stop and output y; this is the gcd of a, b.
4. if r ≠ 0, replace (x, y) by (y,r). Go to step 2.

These are the steps for the division algorithm:

1. Subtract the divisor from the dividend repeatedly until we get a result that lies between 0 and the divisor
2. The resulting number is known as the remainder, and the number of times that the divisor is subtracted is called the quotient.

To find the greatest common divisor of 621 and 259 by the Euclidean algorithm you need to:

• Divide 621 by 259, applying the division algorithm you get
  `621-259=362\\352 - 259 =103`

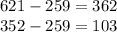
next you need to write the expression
`621 = 259 \cdot 2+103`

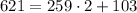
• Divide 259 by 103 to write
  `259=103\cdot 2 +53`

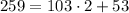
• Divide 103 by 53 to write
  `103=53\cdot 1+50`
• Divide 53 by 50 to write
  `53=50\cdot 1+3`
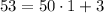
• Divide 50 by 3 to write
  `50=3\cdot 16+2`
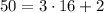
• Divide 3 by 2 to write
  `3=2\cdot 1+1`
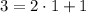
• Divide 2 by 1 to write
  `2=1\cdot 2+0`

The greatest common divisor of 621 and 259 is 1

To find the greatest common divisor of 156 and 108 by the Euclidean algorithm you need to:

• Divide 156 by 108 to write
  `156=108\cdot 1+48`
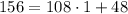
• Divide 108 by 48 to write
  `108=48\cdot 2 + 12`
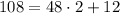
• Divide 48 by 12 to write
  `48=12\cdot 4 +0`

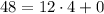
The greatest common divisor of 156 and 108 is 12