Question

The surface areas of two similar figures are given. The volume of the larger figure is given. Find the volume of the smaller figure. S.A. = 192 m S.A. = 1728 m² V = 4860 m3

Answer 1

The volume of smaller figure is 180 m³

Explanation:

Consider the provided information.

The ratio of the surface areas is equal to the square of scale factor K.

let K₁ and K₂ is the scale factor

Thus
`(k^2_1)/(k^2_2) =(S.A_1)/(S.A_2)`

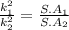
Substitute the respective values as shown.

`(k^2_1)/(k^2_2) =(192)/(1728)`

`(k^2_1)/(k^2_2) =(1)/(9)`

`(k_1)/(k_2) =(1)/(3)`

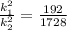
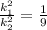
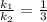
It is given that the volume of larger figure is 4860 m³.

Let V₁ and V₂ is the volume of small and larger figure respectively.

The ratio of the volume is equal to the third power of scale factor K.

Thus
`(k^3_1)/(k^3_2) =(V_1)/(V_2)`

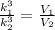
Substitute the respective values as shown.

`(1^3)/(3^3) =(V_1)/(4860)`

`(1)/(27) =(V_1)/(4860)`

`V_1=(4860)/(27)`

`V_1=180`

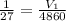
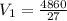
Hence, the volume of smaller figure is 180 m³