Lets consider the symmetric matrix
 , and the two eigenvectors
, and the two eigenvectors
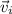 and
and
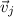 such as:
such as:

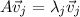
with
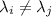 .
.
The dot product between
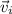 and
and
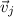 can be obtained with:
can be obtained with:
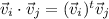
Using the first eigenvector equation we can find:
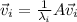
Lets transpose it


as
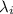 is an scalar
is an scalar
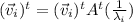
Now, as A is symmetric:
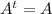
so
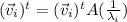
Lets take the dot product again:
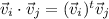
but this is :
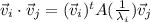

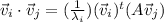
But, the parenthesis is equal to
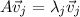
so
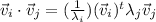
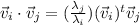
Now, subtracting the dot product
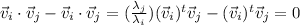
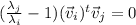
As the eigenvalues are distinct,
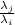 can't be 1, so
can't be 1, so
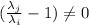
this implies
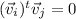
so the eigenvectors are orthogonal.