Answer: We have that
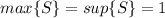 and
and
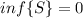 but the minimum of S doesn't exist.
but the minimum of S doesn't exist.
Step-by-step explanation: To find the supremum (or least upper bound) of a set, we first need to prove that an upper bound exists. So we must find a number
 such that
such that
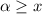 for all
for all
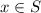 . Note that
. Note that
 for every
for every
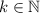 . Thus, for each
. Thus, for each
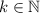 , we have that
, we have that
 . This proves that
. This proves that
 is an upper bound for
is an upper bound for
 . Since the set is bounded above, then we have that the supremum must exist. Notice that
. Since the set is bounded above, then we have that the supremum must exist. Notice that
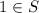 which means 1 is the highest number in
which means 1 is the highest number in
 . So we conclude that
. So we conclude that
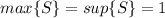 .
.
Now to find the infimum, we must start by finding a lower bound for
 . This will turn out to be quite easy as we just need to notice that if
. This will turn out to be quite easy as we just need to notice that if
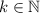 then
then
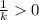 . Now we have our lower bound! This means S is bounded below and thus its infimum exists. Let us claim that
. Now we have our lower bound! This means S is bounded below and thus its infimum exists. Let us claim that
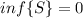 . As per the definition of infimum, we need to prove that any other lower bound would be smaller than 0. This is not so simple so think of it this way: if we find a number greater than 0 that is also a lower bound for S, then 0 is not the greatest lower bound. Then we will set out to prove that any number greater than 0 is not a lower bound. Let us assume then that
. As per the definition of infimum, we need to prove that any other lower bound would be smaller than 0. This is not so simple so think of it this way: if we find a number greater than 0 that is also a lower bound for S, then 0 is not the greatest lower bound. Then we will set out to prove that any number greater than 0 is not a lower bound. Let us assume then that
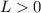 . Then there is some
. Then there is some
 such that
such that
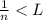 . Since
. Since
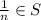 , then
, then
 is not a lower bound for
is not a lower bound for
 . This shows that
. This shows that
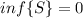 . Recall that when a set has its infimum as an element, we call it minimum but since we've already proven that every element of S is strictly greater than 0, then the minimum of S doesn't exist.
. Recall that when a set has its infimum as an element, we call it minimum but since we've already proven that every element of S is strictly greater than 0, then the minimum of S doesn't exist.