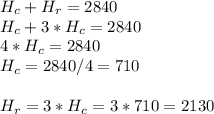Question

Suppose the weekly revenue for a company is given byr: 202400p wherep is the price of their product. What is the price of their product if the weekly revenue is $18,750? 7 8) 8) A company manufactures two types of prefabricated houses ranch and colonial. Last year they sold three times as many ranch models as they did colonial models. If a total of 2840 houses were sold last year, how many of each model were sold?

Answer 1

(a) The price for a revenue of $18,750 is $239.2.

(b) They sold 710 colonial houses and 2130 ranch houses

Explanation:

(a) If the weekly revenue is defined as

`r=2p^2+400p`

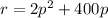
then the price must be calculated as:

`r=2p^2+400p=18750\\\\2p^2+400p-18750=0`

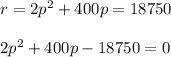
The roots of this function are

`x=(-b\pm √(b^2-4ac))/(2a)=(-400 \pm √(400^2-4*2*(-18750)))/(2*2)\\  \\x=(-400 \pm 556.78)/(4)\\ \\x_1=-39.2\\x_2=239.2`

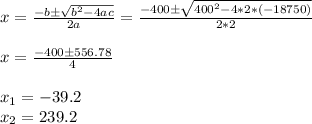
The first root is negative, so it is not a real solution. So the second root is the answer.

The price for a revenue of $18,750 is $239.2.

(b) Last year they sold three times as many ranch models (Hr) as they did colonial models (Hc):

`H_r=3*H_c`

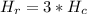
The total amount of houses sold (colonial + ranch) is 2840

`H_c+H_r=2840\\H_c+3*H_c=2840\\4*H_c=2840\\H_c=2840/4=710\\\\H_r = 3*H_c=3*710=2130`