Question

Plz use Differential equation method to solve this:

LaTeX: y'=y+\frac{x}{y};\:\:y\left(0\right)=1

Answer 1

Explanation:

We have the differential equation
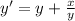`y' = y + (x)/(y)` with initial conditions
`y(0)=1`.

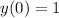First, notice that the equation can be rewritten as

`y'-y =xy^(-1)`,

which is a Bernoulli equation. Once we have recognized the type of the equation we know how to continue. Recall that a Bernoulli equation has the general form

`y'+p(x)y=q(x)y^n`.

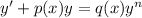In this particular case we have
`n=-1`. This kind of equation is solved by the change of variable
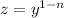`z=y^(1-n)`. In our exercise we get
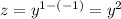`z=y^(1-(-1))=y^2`. Now we take derivatives and get

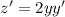`z'=2yy'` which es equivalent to
`(z')/(2y)=y'`.

Then, we substitute the value of
`y'` we have obtained in the original equation:

`(z')/(2y)-y = xy^(-1)`.

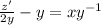The next step is to multiply the whole equation by
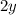`2y`, in order to eliminate the denominator of
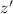`z'`. Thus,

`z' -2y^2=2x`.

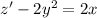Recall that
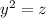`y^2=z`, then

`z' -2z=2x`.

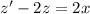This last equation is a linear equation, which has general solution

`z(x) = \exp\left(-\int(-2)dx\right)\left(\int 2x \exp\left(\int(-2)dx + C\right)\right)`.

So, let us calculate the integral that appear in the formula:

`\int(-2)dx = -2x`

`\int 2x e^(-2x)dx = -(\left(2x+1\right)e^(-2x))/(2)`.

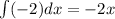
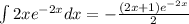Then, the solution for
`z` is

`z(x) = e^(2x)\left(-(\left(2x+1\right)e^(-2x))/(2) + C\right) = -(\left(2x+1\right))/(2) + Ce^(2x)`.

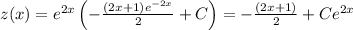Now, we return the change of variable:

`(y(x))^2 =-(\left(2x+1\right))/(2) + Ce^(2x)`.

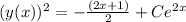The last step is to find the value of the constant
`C`. In order to do this, substitute the initial value:

`(y(0))^2 = 1 =(\left(2\cdot 0+1\right))/(2) + Ce^(2\cdot 0) = -(1)/(2) + C`.

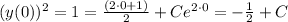Thus, we have the equation

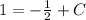`1=-(1)/(2) + C` that gives
`C=(3)/(2)`.

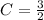Therefore,

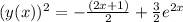`(y(x))^2 = -(\left(2x+1\right))/(2) + (3)/(2)e^(2x)`.