Answer: The degree of (fog)(x) =6
Explanation:
Given:
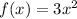
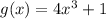
To find:
The degree of (fog) (x)
Solution:
Formula used for calculating fog (x) is given as:
(fog) (x)=[f(g(x))]
Substitute the value of f(x) and g(x) in the above equation, we get
(fog) (x)=
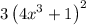
=
![3\left[16 x^(6)+2\left(4 x^(3)+1\right)+1\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hr895omtrxxdwj6p4n967v41c53dqi7yxa.png)
=
![3\left[16 x^(6)+8 x^(3)+2+1\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1zms224x75okjjyxvum2qu0fza5xv269je.png)
=
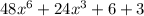
=
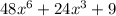
(fog) (x)=
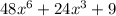
Result:
The degree of (fog) (x)=
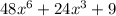 is Six.
is Six.